מדריך הידע של SR Flip-Flop-עקרון עבודה, יתרונות, חסרונות, טבלת אמת והבדלים מ- RS Flip-flop
כפכף הוא פשוט מונח המתייחס למכשיר אלקטרוני דיגיטלי, שהוא רכיב אלקטרוני המשמש לאחסון מידע יחיד.
ה- Sr Flip-Flop (Set-reeset-Flip-Flop) הוא רכיב בסיסי במעגלים אלקטרוניים דיגיטליים המשמשים לאחסון ולתמרון נתונים.זה פועל באופן רציף.ניתן לבנות כפכפים של SR באמצעות תפסים של SR.תפס הוא מעגל אלקטרוני דיגיטלי שלוקח צורה פשוטה של אלמנט אחסון, המסוגל לאחסן מעט מידע בינארי (0 או 1).במאמר זה נדון בכפכף ה- SR, כולל עקרון העבודה, טבלת האמת, היתרונות, החסרונות וההבדלים מהכפכפים של RS.
קָטָלוֹג
1. עקרון העבודה של SR Flip-Flop
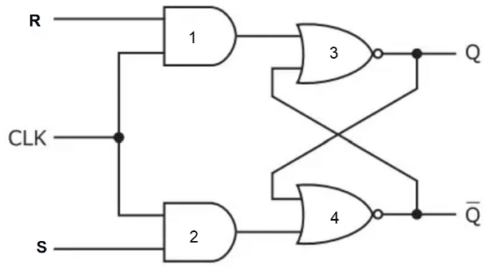
ניתן לבנות את הכפכתה הפשוטה ביותר של RS באמצעות שני שערים של שני כניסה ולא, כפי שמוצג בתרשים:
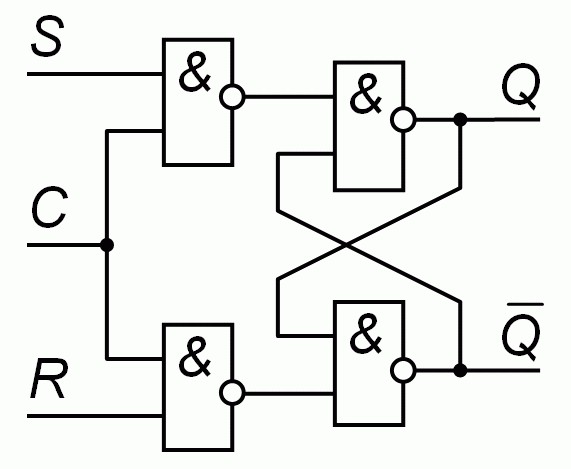
שימו לב כי האופן בו האלמנטים מחוברים מבטיח שהם תמיד נמצאים במדינות הפוכות.אם הפלט של האלמנט הראשון הוא 1, הפלט של האלמנט השני יהיה 0, ולהיפך.
כדי להקל על ההבנה, הנה ארבעת התרחישים שיכולים להתרחש עם כפכף SR:
תרחיש 1: S = 0, r = 0
פלט שער: פלט GATE1 וגם GATE2 0. תחזוקת מצב: מכיוון ששערים 3 ו -4 הם לא שערים, עם קלט אחד ב 0, תפוקותיהם תלויות בכניסה השנייה.לפיכך, GATE3/Q (N+1) שומר על המצב הקודם Q, ו- GATE4/Q (N+1) 'שומר על המצב המשלים Q'.
תרחיש 2: S = 0, r = 1
פלט GATE: GATE1 יציאות 1 (מכיוון ש- R גבוה), יציאות GATE2 0. איפוס הפעלה: עבור GATE3, כניסה אחת גבוהה (מ- GATE1), מה שמוביל לפלט של 0 דרך הפעולה NOR, ובכך מאפס את המדינה.עם זאת, קלט אחד ל- GATE4 נותר נמוך, מוציא 1, ומציין את המצב המשלים.
תרחיש 3: S = 1, r = 0
פלט שער: GATE1 יציאות 0, GATE2 יציאות 1 (מכיוון ש- S גבוה).פעולת הגדרת: בשלב זה, יציאות GATE3 1 (הקלט האחר מ- GATE1 נמוך), ומגדיר את הכפכף.לעומת זאת, בגלל הקלט הגבוה מ- GATE2, GATE4 מוצא 0, המאשר את המצב המשלים.
תרחיש 4: S = 1, r = 1
פלט שער: עם שתי הכניסות גבוהות, שני השערים פלט 1. מצב לא חוקי: כאשר שתי הכניסות גבוהות, שערים 3 ו -4 שניהם פלט 0, וכתוצאה מכך סכסוך מכיוון ש- q (n+1) ו- q (n+1) 'צריכיםהיו תפוקות משלימות, אך זה לא המקרה, מה שמוביל לכך שמדינה זו אינה תקפה.
2. טבלת האמת של כפכף SR
|
ס |
ר ' |
ש (n+1) |
מדינה |
|
0 |
0 |
Qn |
ללא שינוי |
|
0 |
1 |
0 |
אִתחוּל |
|
1 |
0 |
1 |
מַעֲרֶכֶת |
|
1 |
1 |
איקס |
לא חוקי |
אנו נשתמש בטבלת האמת הזו כדי לכתוב את הטבלה האופיינית עבור כפכפי ה- SR.בטבלת האמת, תוכלו לראות שתי תשומות, S ו- R, ופלט אחד, Q (n+1).עם זאת, בטבלה האופיינית, תוכלו לראות שלוש תשומות, S, R ו- QN, ופלט אחד, Q (n+1).
מתרשים ההיגיון, ברור ש- QN ו- QN 'הם שני תפוקות משלימות, הפועלות גם ככניסות לשערים 3 ו -4, ולכן אנו רואים את QN, המצב הנוכחי של הכפכף, כקלט, ו- Q (n+1), המצב הבא, כפלט.
לאחר כתיבת הטבלה האופיינית, נצייר מפת K-משתנה 3-משתנה כדי להפיק את המשוואה האופיינית.
3. טבלה אופיינית
|
ג |
ר ' |
Qn |
ש (n+1) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
איקס |
|
1 |
1 |
1 |
איקס |
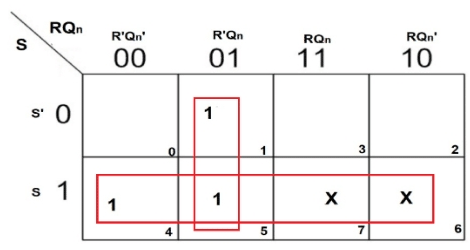
ממפת ה- K אתה מקבל שני זוגות.לאחר פתרון שניהם, אנו משיגים את המשוואה האופיינית הבאה:
Q (n + 1) = s + r'Qn
4. יתרונות של כפכף SR
באמצעות כפכפי SR יש מספר יתרונות.להלן חלקם:
- פשטות: העיצוב של כפכפי SR הוא פשוט יחסית, המורכב רק מכמה שערים.ניתן לשלב אותם בקלות במעגלים גדולים יותר מבלי לסבך את העיצוב הכללי.
- מהירות: כפכפי SR פועלים במהירות גבוהה.הם יכולים לעבור במהירות בין מצבים מוגדרים לאיפוס ללא עיכוב, ולהבטיח שמערכות דיגיטליות יכולות לבצע משימות בצורה יעילה יותר, ובכך לשפר את הביצועים של טכנולוגיות המסתמכות על עיבוד נתונים מהיר.
- צריכת חשמל נמוכה: כפכפי SR צורכים מעט מאוד כוח, מה שהופך אותם לאידיאליים לשימוש במכשירים המונעים על סוללות, כמו טלפונים ניידים ומכשירי מחשוב ניידים, ובמקביל משמעות גם עלויות תפעוליות נמוכות יותר מבחינת השימוש באנרגיה.
- פעולה ניתנת לביטוס: כפכפי SR יכולים לשמור על מצב ללא הגבלת זמן (להגדיר או לאפס) עד שאות קלט יבקש שינוי, והיכולת לשמור על מצב יציב ללא קלט קבוע הופכת את כפכפי SR לשימוש ליישומים שונים.
5. מגבלות כפכפי SR
למרות מספר יתרונות, לכפכפי SR יש גם מגבלות מסוימות.להלן חלקם:
- תנאי מירוץ: כפכפי SR רגישים לתנאי מירוץ בהם מצב התפוקה עשוי להשתנות באופן בלתי צפוי בגלל שינויים בתזמון אותות קלט, מה שעלול להוביל לשגיאות או לתוצאות בלתי צפויות.
- מצב לא חוקי: מגבלה מובנית של כפכפי SR היא התנהגותם כאשר גם הסטים (ים) וגם כניסות האיפוס (R) פעילים בו זמנית.במקרה זה, הכפכף נכנס למצב לא חוקי, וכתוצאה מכך שתי התפוקות היו גבוהות או נמוכות, מה שמפר את עקרון ההפעלה הבסיסי של מכשיר בביסט.מצב לא חוקי זה יכול לשבש את הפונקציה הרגילה של מעגלים דיגיטליים, מה שמוביל להתנהגות מערכת בלתי צפויה ולאובדן נתונים פוטנציאלי.
- מדרגיות מוגבלת: כפכפי SR עשויים להיות קשים לקנה מידה למערכות דיגיטליות מורכבות יותר ככל שהמורכבות של המערכת גדלה, הסבירות להציג טעויות בגלל האופי הבסיסי של כפכפי SR עולה גם כן.
6. אזורי יישום
- מערכות בקרה: במערכות בקרה, כפכפי SR יכולים להשיג מעברים חלקים בין אותות, ובכך למזער את סיכוני התאונות ולשיפור זרימת התנועה.יישום נפוץ נמצא במערכות בקרת רמזור, כאשר כפכפי SR עוזרים בניהול רצף הרמזורים, ומבטיחים שהאותות משתנים באופן מדויק ומסודר, ובכך בשליטה על זרימת התנועה בבטחה וביעילות.
- אחסון זיכרון: כפכפי SR הם גם רכיבים בסיסיים של התקני אחסון זיכרון כמו רישומים.הם משמשים לאחסון באופן זמני נתונים במכשירי מחשוב שנעים בין מעבדי מיקרו -מעבדים למעבדי אות דיגיטליים, ומאפשרים גישה מהירה ומניפולציה של נתונים במהלך משימות עיבוד.
- דלפקים דיגיטליים: כפכפי SR משמשים במונים דיגיטליים לספירת פעולות, ומאפשרים צמיחה או ירידה בהתבסס על אותות קלט.
- סנכרון נתונים: כפכפי SR הם מכריעים לסנכרון אותות נתונים בין שני מעגלים דיגיטליים, ומבטיחים שהם פועלים בו זמנית באותו מחזור שעון, מה שמועיל מאוד לשמירה על אמינות רשתות התקשורת.
- מתנדים: בשילוב עם רכיבים אחרים, כפכפי SR יכולים ליצור מתנדים פשוטים המייצרים אותות תקופתיים.זה שימושי במיוחד ביישומים כמו מעגלי שעון ומחוללי אות שמע בהם יש צורך בייצור אותות עקבי ויציב.
7. הבדלים בין כפכפי SR ו- RS
|
תכונה |
כפכף SR |
RS כפכפים |
|
S = 0 , R = 0 |
Q מצב (ללא שינוי) נשמר. |
Q מצב (ללא שינוי) נשמר. |
|
S = 0 , R = 1 |
איפוס (q = 0) |
איפוס (q = 0) |
|
S = 1 , R = 0 |
הגדר (q = 1) |
הגדר (q = 1) |
|
S = 1 , R = 1 |
הגדר (דומיננטי) (q = 1) |
איפוס (דומיננטי) (q = 0) |
|
יתרונות: |
כאשר S ו- R הם שניהם 1, פעולת הסט
מקבל עדיפות. |
כאשר S ו- R הם שניהם 1, פעולת האיפוס
מקבל עדיפות. |
עלינו
ALLELCO LIMITED
קרא עוד
חקירה מהירה
אנא שלח בירור, נגיב מייד.
→ קודם

סוללות AG1 מתעלמות לעתים קרובות אך משמעותיות מאוד, ממריצות מגוון מכשירים מגאדג'טים יומיומיים לציוד רפואי.סוללות AG1, הזמינות הן בגרסאות אלקליות והן בגרסאות תחמוצת הכס...

הבנת יכולת הסוללה של המכונית שלך וכיצד היא מתפקדת בתנאים מגוונים חשובה לכל בעל רכב, במיוחד כאשר הוא מתמודד עם אתגרי מזג אוויר קיצוניים.דירוג AMPs (CCA) הקרים (CCA) הוא מדד ח...
→ הַבָּא

החלפות שוות סוללה של AG1
ב- 2024/04/27

כמה אתה יודע על CCA?
ב- 2024/04/26
פוסטים פופולריים
-
מה זה GND במעגל?
ב- 1970/01/1 2946
-

מדריך מחברים RJ-45: RJ-45 קודי צבע מחבר, תוכניות חיווט, יישומי R-J45, גיליון נתונים RJ-45
ב- 1970/01/1 2502
-

סוגי מחברי סיבים: SC לעומת LC ו- LC לעומת MTP
ב- 1970/01/1 2091
-
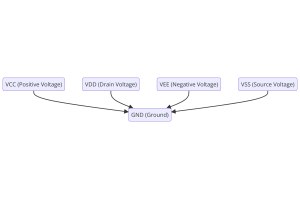
הבנת מתחי אספקת חשמל ב- Electronics VCC, VDD, VEE, VSS ו- GND
ב- 0400/11/9 1898
-

השוואה בין DB9 ל- RS232
ב- 1970/01/1 1765
-

מהי סוללת LR44?
חשמל, אותו כוח בכל מקום, מחלחל בשקט כל היבט בחיי היומיום שלנו, מגאדג'טים טריוויאליים ועד ציוד רפואי מסכן חיים, הוא ממלא תפקיד שקט.עם זאת, באמת לתפוס את האנרגיה הזו, במיוחד כיצד לאחסן ולהפוך אותה ביעילות, זו לא משימה קלה.זה ע...ב- 1970/01/1 1714
-

הבנת היסודות: התנגדות השראות, וציון
בריקוד המורכב של הנדסת חשמל, שלישיית אלמנטים בסיסיים עולה במרכז הבמה: השראות, התנגדות וקיבול.כל אחת מהן נושאת תכונות ייחודיות המכתיבות את המקצבים הדינמיים של מעגלים אלקטרוניים.כאן אנו יוצאים למסע לפענוח המורכבות של רכי...ב- 1970/01/1 1662
-

מדריך מקיף של CR2430 סוללה: מפרט, יישומים והשוואה לסוללות CR2032
מהי סוללת CR2430?היתרונות של סוללות CR2430נוֹרמָהיישומי סוללה CR2430CR2430 שווה ערךCR2430 לעומת CR2032גודל CR2430 סוללהמה לחפש בעת קניית CR2430 ושוויוןגיליון נתונים PDFשאלות נפוצות סוללות הן לבם של מכשירים אלקטרוניים קטנים.בין הסוגים הרבים הק...ב- 1970/01/1 1567
-
מה זה RF ולמה אנו משתמשים בזה?
טכנולוגיית תדר רדיו (RF) היא חלק מרכזי בתקשורת אלחוטית מודרנית, המאפשרת העברת נתונים למרחקים ארוכים ללא חיבורים פיזיים.מאמר זה מתעמק ביסודות ה- RF, ומסביר כיצד קרינה אלקטרומגנטית (EMR) מאפשרת תקשורת RF.נחקור את עקרונות ה- EMR, את...ב- 1970/01/1 1550
-

CR2450 לעומת CR2032: האם ניתן להשתמש בסוללה במקום זאת?
לסוללות ליתיום מנגן יש כמה קווי דמיון עם סוללות ליתיום אחרות.צפיפות אנרגיה גבוהה וחיי שירות ארוכים הם המאפיינים המשותפים להם.סוללה מסוג זה זכתה באמון ובחובם של צרכנים רבים בגלל בטיחותה הייחודית.גאדג'טים טכניים יקרים?מכ...ב- 1970/01/1 1519















































