בית בלוג~~מדריך מפורט ל- Adder מלא~~

~~ב- 2024/05/10~~ ~~626~~

מדריך מפורט ל- Adder מלא

בתחום האלקטרוניקה הדיגיטלית והנדסת מחשבים, תוספות מייצגות את אחד מאבני הבניין החיוניות ביותר, מרכזי בבנייה ופונקציונליות של מעגלים אריתמטיים מורכבים יותר.כרכיבים אינטגרליים של יחידת ההיגיון האריתמטית (ALU), תוספים מקלים על פעולות מחשוב רבות, החל מחשבון בסיסי למשימות לוגיות מורכבות הנחוצות לפעולות מערכת.העיצוב שלהם, שיכול להשתנות מחצי תוספת פשוטים לתוספים מלאים מורכבים יותר, ממלא תפקיד מכריע בשיפור היעילות ומהירות העיבוד במערכות דיגיטליות.מאמר זה מתעמק בארכיטקטורה המפורטת וניואנסים פונקציונליים של סוגים שונים של מוסיפים, וממחישים את תפקידם הקריטי בטכנולוגיית המחשוב המודרנית ובוחן את ההיגיון, המעגלים והיישומים התפעוליים שלהם בהקשר הרחב יותר של עיצוב לוגי דיגיטלי.

קָטָלוֹג

1. מהו ADDER?

2. חצי אד

3. Adder מלא

4. טבלת אמת מלאה של Adder

5. משוואות מאפיינים של אדר מלא

6. יישום מעגל Adder מלא

7. יתרונות וחסרונות של תוספים מלאים

8. יישומים של תוספים מלאים בהיגיון דיגיטלי

9. דוגמאות ליישומי ADDER מלאים

10. מסקנה

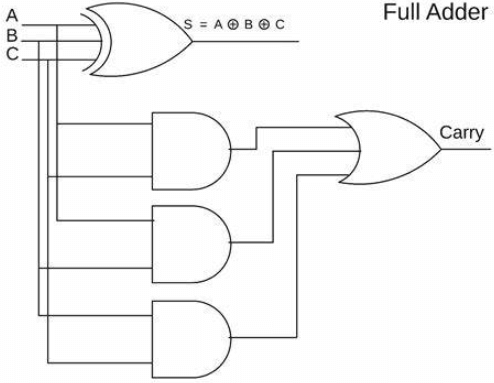
איור 1: Adder מלא

מהו ADDER?

ADDER הוא רכיב בסיסי בהנדסת אלקטרוניקה ותכנון לוגיקה דיגיטלית וממלא תפקיד מרכזי במערכות מחשב מורכבות יותר.כחלק מיחידת ההיגיון האריתמטית (ALU), ה- ADDER מטפל במגוון משימות מחשוב חיוניות.היעילות והביצועים של המעבד כולו מושפעים ישירות מהתכנון והפונקציונליות של ה- ADDER.

במעבד, ה- ADDER משמש לא רק לפעולות חשבון בסיסיות כמו תוספת וחיסור, אלא הוא גם עוסק במגוון רחב יותר של פעולות לוגיות.לדוגמה, בעת הפעלת תוכניות, המעבד לעתים קרובות צריך לחשב כתובות זיכרון חדשות.בדרך כלל זה נעשה על ידי הוספת או חיסור מהכתובת הנוכחית - משימה שביצעה ה- ADDER.הם שולטים במספר איטרציות הלולאה והזרימה הכוללת על ידי הגדלת דלפקים וירידה.ביישומים מורכבים יותר, כגון אינדקס טבלאות, תוספות מאתרות במהירות נתונים על ידי חישוב קיזוזים.זה חשוב למערכות ניהול מסדי נתונים, בניית מהדר ועיבוד נתונים בקנה מידה גדול.תוספים הם גם המפתח ביישום טכניקות מיפוי מסוימות במערכות מטמון רב-רמות, תוך שימוש בפעולות חשבון כדי לקבוע את מיקום הנתונים במטמון, ובכך מיטבים את יעילות הגישה.

מבחינה טכנולוגית, תוספות מיושמות באמצעות עיצובים שונים של מעגלים כולל תוספות מקבילות, סדרתיות וצינורות.תוספות מקבילות מועדפות על יכולתם להתמודד עם מספר ספרות בו זמנית, מה שהופך אותם להתאים לתרחישים הדורשים חישוב מהיר.לעומת זאת, תוספים סדרתיים מעבדים סיביות אחת לכל מחזור שעון והם אידיאליים לסביבות מוגבלות משאבים או בעלות עוצמה נמוכה.תוספי צנרת מחלקים את תהליך התוספת למספר שלבים, שכל אחד מהם מטפל בחלק מפעולת התוספת.תכנון זה מגביר משמעותית את מהירות החישוב, במיוחד בסביבות מחשוב בעלות ביצועים גבוהים.

חצי אדר

מעגל חצי-סדר הוא אבן בניין בסיסית באלקטרוניקה דיגיטלית, שתוכננה במיוחד להוסיף שתי ספרות בינאריות בודדות.מעגל זה מהווה את הבסיס של ADDER מלא והוא המפתח להבנת עיצובי מעגלי לוגיקה מורכבים יותר.בחצי מדרדר, ישנן שתי כניסות עיקריות, שכותרתו A ו- B, המייצגות את ה- AGOND ואת התוספת בהתאמה.הגדרה זו מאפשרת לו לחשב את הסכום ולשאת פלט ללא צורך בקלט נשיאה מחישובים קודמים.

הליבה של חצי סדר מורכבת משני שערי לוגיקה: שער XOR ושער ושער.שער ה- XOR אחראי לייצור תפוקת הסכום.זה פועל תחת כלל פשוט בו הוא מוציא 1 אם רק אחת מהכניסות שלו היא 1;אחרת, הוא מוציא 0. השער והשער, לעומת זאת, מטפל בתפוקת הנשיאה.הוא מייצר 1 רק כאשר שתי התשומות שלה הן 1, המתאימות בצורה מושלמת לדרישות הבסיסיות של תוספת בינארית.

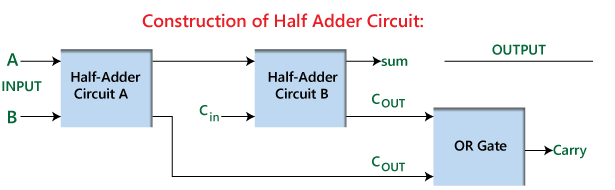
איור 2: בניית חצי אדדר

תכנון יעיל ופשוט זה מאפשר לחצי ADDER לא רק לבצע תוספת בינארית בסיסית באופן עצמאי, אלא גם לשמש אבן בניין ליצירת ADDER מלא.ADDER מלא בנוי על ידי שילוב של שני תוספים של חצי תוספים עם נוסף או שער.בהגדרה זו, המחצית הראשונה של Adder מקבלת את משימת התוספת הראשונית, ומייצרת סכום ראשוני ונשיאה.לאחר מכן מחצית המחצית השנייה מעבדת את הנשיאה מהראשון יחד עם קלט נשיאה נוסף.לבסוף, השער או ממזג את שתי תפוקות הנשיאה כדי לייצר את תפוקת הנשיאה הסופית.סידור זה משפר את הפונקציונליות של ה- ADDER, ומאפשר לו לטפל במשימות תוספת מרובות סיביות מורכבות יותר, ומציג את היישום הנרחב וחשיבותם של חצי תוספים בעיצוב מעגלים דיגיטליים.

Adder מלא

ADDER מלא הוא רכיב מתקדם בעיצוב לוגיקה דיגיטלית, המצויד להתמודד עם תוספת של שלוש כניסות בינאריות בודדות, המתויגות בדרך כלל כ- A, B ו- Carry-In (CIN).תכנון זה מאפשר למלאה המלא לעבד ביעילות תוספות בינאריות מורכבות על ידי שילוב הנשיאה מחישובים קודמים בסדר גודל נמוך יותר לפעולה יחידה.

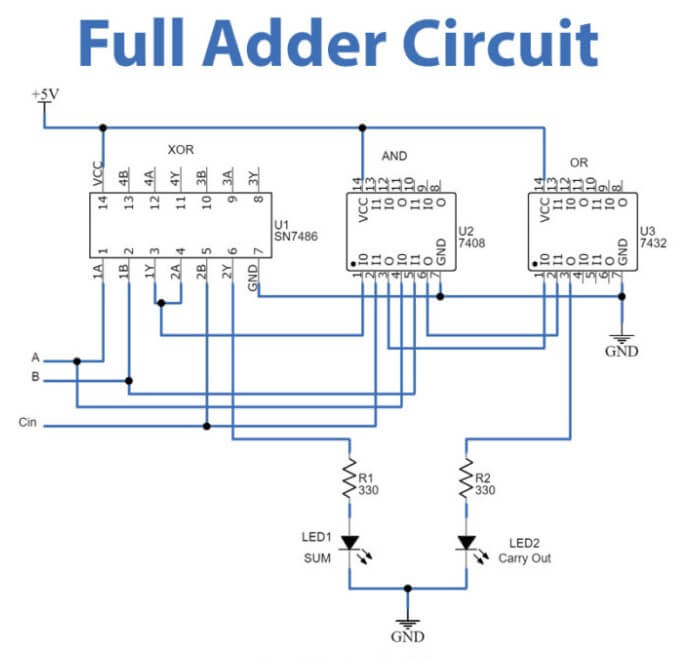
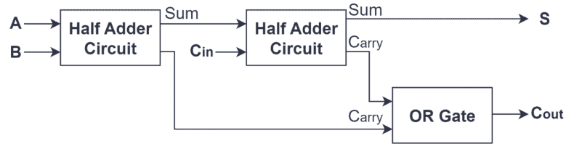
איור 3: מעגל Adder מלא

מבחינה פונקציונלית, ADDER מלא יכול להפיק סכום דו ספרתי, מה שאומר שהפלט שלו יכול לנוע בין 0 ל -3, והוא יכול גם לייצר נשיאה (COUT).זה קורה מכיוון שכאשר כל סיביות הקלט מוגדרות ל- 1 (a = 1, b = 1, cin = 1), תפוקת הסכום תהיה 1 (המייצג 01 בינארי), ונוצר נשיאה של 1, מה שמצביע על כךיש להעביר נשיאה נוספת לקטע הגבוה הבא.

מבחינה מבנית, המלא המלא מורכב בדרך כלל משני מוסיפים חצי ושער אחד או שער.Adder של המחצית הראשונה מקבלת תשומות A ו- B, ומייצרת סכום ראשוני ואות נשיאה.לאחר מכן ניזונים הסכום הראשוני הזה, יחד עם ההובלה (CIN), לחצי המחצית השנייה.תפקידו של המחצית השנייה של Adder הוא להוסיף את הסכום הזה מהמחצית הראשונה ל- CIN, לייצר סכום נוסף ופלט נשיאה חדש.במקביל, תפוקת הנשיאה מהמחצית הראשונה ותפוקת הנשיאה מהמחצית השנייה ממוזגת דרך שער או שער, ומגיעים לשיאם במשיכה הסופית (COUT) של המלא המלא.תכנון מבנה זה מבטיח כי המלא המלא מטפל ביעילות על התפשטות נשאים בנוסף על פעולות, מה שהופך אותו לאידיאלי לביצוע תוספות בינאריות רב-סיביות.לפיכך, תכנון המלא המלא לא רק מזרז את עיבוד הנתונים ומשפר את היעילות אלא גם מפשט את המורכבות של יישום החומרה באמצעות שילוב פשוט של שערי לוגיקה, מה שהופך אותו למרכיב חיוני בתוספת רב-ספרתית ויחידת הלוגיקה האריתמטית (Alu).

פרמטרים	חצי אדר	Adder מלא
תיאור	חצי אדדר הוא היגיון משולב מעגל שמוסיף שתי ספרות של 1 סיביות.החצי-סדר מייצר סכום מהשניים תשומות.	Adder מלא הוא היגיון משולב מעגל שמבצע פעולת תוספת בשלושה מספרים בינאריים של סיביות. ה- ADDER המלא מייצר סכום משלוש התשומות וערך הנשיאה.
נשיאה קודמת	הנשיאה הקודמת אינה משמשת.	נעשה שימוש בסחיבה הקודמת.
תשומות	במחצית Adder, ישנם שני ביטים קלט (א, ב).	ב- Adder מלא, ישנם שלושה חתיכות קלט (א ב ג_ב).
תפוקות	הפלט שנוצר הוא של שני ביטים סכום ונשא מהקלט של 2 ביטים.	הפלט שנוצר הוא של שני ביטים סכום ונשא מהקלט של 3 ביטים.
משמש כ	לא ניתן להשתמש במעגל חצי-אדן באותו אופן במעגל עדר מלא.	ניתן להשתמש במעגל Adder מלא במקום של מעגל Adder של חצי.
תכונה	זה פשוט וקל ליישום	העיצוב של אדר מלא אינו כמו פשוט כמו חצי אד.
ביטוי לוגי	הביטוי ההגיוני עבור חצי אדדר הוא: S = a⊕b;C = a*b.	ביטוי לוגי עבור Adder מלא הוא: S = a⊕b⊕cin;ג_{הַחוּצָה}= (ab)+(c_ב(a⊕b)).
שערים לוגיים	זה מורכב משער לשעבר אחד או אחד ו שַׁעַר.	זה מורכב משני או לשני, שניים ושערים, ושער אחד או שער.
יישומים	הוא משמש במחשבים, מחשבים, מכשירי מדידה דיגיטליים וכו '.	הוא משמש בתוספות מרובות סיביות, מעבדים דיגיטליים וכו '.
שם חלופי	אין שם חלופי למחצית פֶּתֶן.	ADDER מלא ידוע גם בשם נשיאת אדווה פֶּתֶן.

טבלה 1: ההבדל בין חצי המדרדר לבין ADDER מלא

טבלת אמת מלאה של Adder

טבלת האמת של ADDER מלא היא המפתח להבנת ההיגיון התפעולי שלו, ומפרט את הקשר המדויק בין שילובי קלט בינארי לבין תפוקותיהם המתאימות.טבלה זו מדגימה את כל תרחישי הקלט הפוטנציאליים ותוצאותיהם, מה שהופך אותה לכלי חיוני בעיצוב ואימות של מעגלי לוגיקה דיגיטליים.ה- ADDER המלא מעבד שלוש תשומות: A, B ו- A CARING-In (CIN), שכל אחד מהם יכול להיות 0 או 1. זה מביא לשמונה שילובים אפשריים של תשומות.

עבור כל אחד מהשילובים הללו, התפוקות מה- ADDER המלאות כוללות סכום (סכום) וניתוח (COUT).הסכום הוא תוספת המודולו-2 (פעולת XOR) של שלוש התשומות-A, B ו- CIN.העבירה מתרחשת כאשר לפחות שניים מקטעי הקלט הם 1. זה משקף את יכולתו של המלאה של המלא לטפל בהעברה בפעולות תוספת רצופות, מה שמבטיח דיוק בחישובים בעלי סיביות גבוה יותר.

כדי להמחיש, שקול את תרחיש הקלט בו כל הכניסות הן 0 (a = 0, b = 0, c-in = 0).סכום הפלט יהיה 0, והנשיאה תהיה גם 0, מה שמצביע על כך שאין סכום נוסף או נשיאה לניהול.אם רק סיביות קלט אחד היא 1, כגון A = 1, B = 0, C-in = 0, סכום הפלט יהיה 1 ללא נשיאה, ומראה כי אין צורך להעביר נשיאה לקטע גבוה יותר.כאשר שני סיביות קלט הם 1, כמו a = 1, b = 1, c-in = 0, סכום הפלט הוא 0 (מכיוון ש- 1+1 שווה 2 בבינארי, ומודולו 2 מביא ל -0), אך העבירה-החוצה הוא 1, המציין נשיאה שצריך לעבור לקטע הגבוה הבא.התרחיש המורכב ביותר מתרחש כאשר כל שלושת סיביות הקלט הם 1 (a = 1, b = 1, c-in = 1);סכום התפוקה הוא 1, ויש נשיאה של 1, מה שמרמז כי יתכן ויהיה צורך בניהול נשיאה בקטעים גבוהים עוד יותר.

א	ב	ג_ב	ג	ג_{הַחוּצָה}
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

תרשים 2: טבלת אמת מלאה של Adder

מאפיינים משוואות של אדר מלא

הבנת המלא המלא כרוכה בניתוח הפונקציונליות שלו באמצעות טבלת האמת, כאשר שילובים שונים של ערכי קלט A, B ו- C-in מובילים לתפוקות סכום ו- COUT.כדי לתפוס את הפעולה, אנו מפשטים את משוואות ההיגיון שלב אחר שלב.

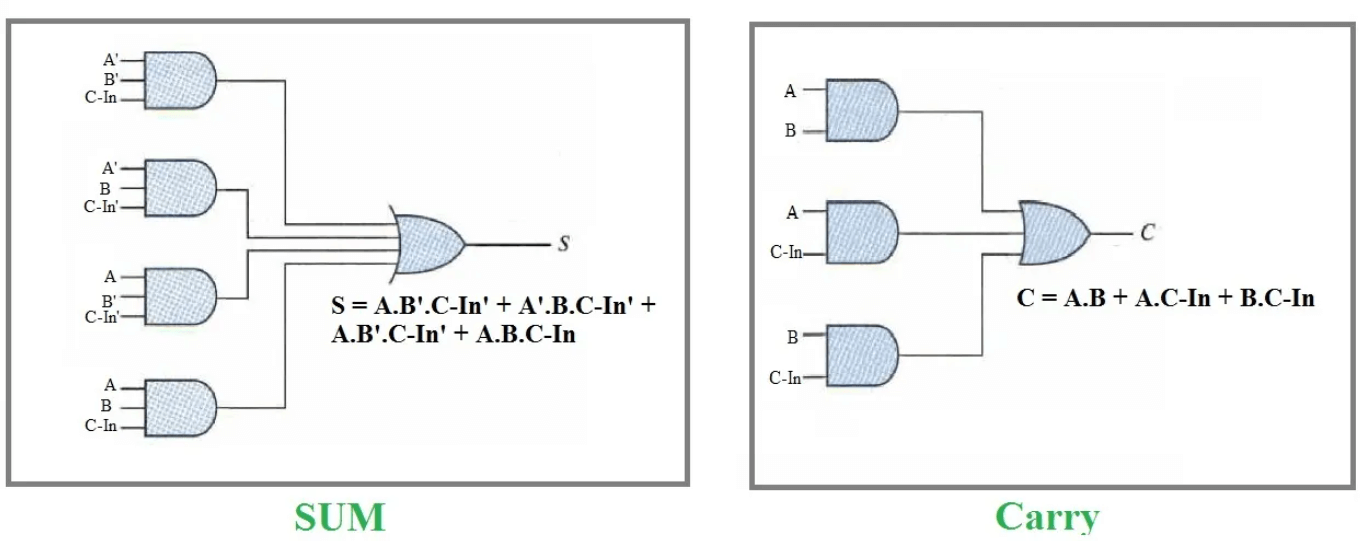
ביטוי לוגי לסכום

המשוואה מתחילה במקרים המובחנים שבהם הסכום שווה ל -1:

• a 'b' cin + a 'b cin' + a b 'cin' + ab cin

ניתן לעיבות משוואה זו על ידי קיבוץ מונחים עם ובלי CIN:

• CIN (A 'B' + AB) + CIN '(A' B + A B ')

פשט זה מוביל לצורה קלה יותר ליישום:

• CIN XOR (A XOR B)

ייצוג זה מראה כי תפוקת הסכום היא למעשה פעולת ה- XOR בקרב A, B ו- CIN, לוכדת את התנהגות הליבה של תוספת בינארית בה סכום מתנגד על בסיס מספר אי -זוגי של אלה.

היגיון ל- COUT

החל מתנאים שבהם נוצרת הנשיאה:

• A 'B CIN + A B' CIN + AB C-in ' + AB CIN

בפישוט המשוואה אנו מזהים מונחים הכרוכים בדרך כלל ביצירת נשיאה:

• AB + B CIN + A CIN

מחפש שיטה אחרת ליישום COUT, ניתן לארגן מחדש את המשוואה:

• ab + cin + b c-in (a + a ')

זה מרחיב ומרחיב מחדש מחדש כדי לתפוס את כל התרחישים שבהם לפחות שתי כניסות הן 1:

• ab cin + ab + a c-in + a 'b cin

• ab (1 + cin) + a-in + a 'b cin

• ab + a c-in (b + b ') + a' b cin

• ab + a b 'cin + a' b cin

• AB + CIN (A 'B + A B')

הטופס הקומפקטי הסופי ל- COUT:

• ab + cin (a xor b)

גרסה זו של משוואת הנשיאה מדגימה כיצד מיוצר COUT כאשר גם A ו- B הם 1, או כאשר אחד מ- A או B הוא 1 יחד עם קביעה, ובכך מכסה את ההיגיון הדרוש לניהול התפשטות נשיאה במולטי-תוספת בינארית ביט.היגיון יעיל זה שימושי במיוחד ליישום מעגלים דיגיטליים יעילים.

איור 4: משוואות של אדר מלא

יישום מעגל ADDER מלא

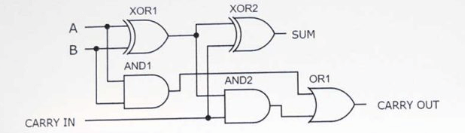
יישום מעגל ADDER מלא כרוך בהרכבה בזהירות של שני מוסיפים חצי ושער ליצירת מכשיר המסוגל לטפל ביעילות בתוספת של שלוש כניסות בינאריות בודדות.סידור זה מייעל את המורכבות של המעגל ומבטיח חישובים יעילים ומדויקים כאחד.

כדי להתחיל, המחצית הראשונה של Adder מקבלת שתי תשומות בינאריות עיקריות, A ו- B, שהן הספרות העיקריות שיש להוסיף.משימת המפתח שלה היא לחשב את הסכום ואת הנשיאה הראשונית של שני המספרים הללו.כאן, Adder המחצית הראשונה מספקת שתי תוצאות: סכום ראשוני (SUM1) ונשיאה ראשונית (Carry1).SUM1 נגזר מפעולת ה- XOR של A ו- B, המציין אם לסך הכל יש מספר משונה של 1.Carry1, התוצאה של הפעולה בין A ו- B, מציינת אם שתי הספרות הן 1, המחייבות נשיאה לקטע הגבוה הבא.

בשלב הבא, המחצית השנייה Adder מצטרפת לתהליך.הוא משתמש ב- Sum Output Sum1 וב- CIN הקלט השלישי (העבר מחישוב קודם) ככניסותיו.Adder של המחצית השנייה מייצר שתי תפוקות: תוצאת הסכום הסופי (SUM2) והנשיאה המשנית (Carry2).SUM2, שהיא תוצאת ה- XOR של SUM1 ו- CIN, מייצגת את הסכום הסופי של שלוש הכניסות, ומציגה את התוספת הבינארית המצטברת.Carry2, העולה מהפעולה בין SUM1 ל- CIN, מצביע על נשיאה שנוצרת על ידי רכיבים אלה.

Full Adder Circuit with Using Two Half Adder

איור 5: מעגל ADDER מלא עם שימוש בשני חצי אדר

לבסוף, כדי להשלים את העיצוב המלא של Adder, נדרש שער או שער כדי לטפל בתפוקות הנשיאה Carry1 ו- Carry2 משני חצי התוספים.זה או שער מבטיח כי כל נשיאה שנוצרת במהלך החישובים מועברת כראוי לפלט הסופי.לפיכך, תפוקת הנשיאה הסופית המלאה של המלא (COUT) היא או תוצאה של Carry1 ו- Carry2.הכללתם של שער זה או שער מבטיחה כי כל הנושאים הפוטנציאליים מחושבים במדויק ומועברים לשלב הבא בפעולות תוספת רב-סיביות, מה שמבטיח את שלמות הפעולה האריתמטית על פני מספר ביטים.

יתרונות ואתגרים של תוספים מלאים בהיגיון דיגיטלי

תוספים מלאים ממלאים תפקיד חיוני בעיצוב ההיגיון הדיגיטלי, ומציעים יתרונות רבים שהופכים אותם לחיוניים בתרחישים שונים של מחשוב ועיבוד נתונים.היתרונות העיקריים שלהם כוללים גמישות מדהימה, מהירויות עיבוד מהירות וניהול נשיאה יעיל.תכונות אלה הופכות תוספים מלאים לאידיאליים לביצוע פעולות אריתמטיות מורכבות ופונקציות לוגיקה, במיוחד ביישומים הדורשים תוספת רב-סיביות רצופות.

יתרונות

גמישות: תוספים מלאים מצטיינים ביכולתם לעבד כניסות בינאריות מרובות (A, B ו- CIN) בו זמנית.ניתן להרחיב אותם גם למערכי Adder גדולים יותר כדי להתמודד עם מספרים בינאריים ארוכים יותר.מדרגיות זו חשובה לבניית יחידות לוגיקה אריתמטיות בעלות ביצועים גבוהים (ALUS), אשר חייבים לבצע פעולות אריתמטיות רב-סיביות מורכבות.

מהירות: בזכות ארכיטקטורת העיבוד המקבילה הפנימית שלהם, תוספות מלאות יכולות להשלים את התוספת של כל הכניסות במחזור שעון יחיד תוך קביעת תפוקות לשאת.יכולת זו תומכת בפעולות תוספת רציפות והיא הכרחית לעיבוד נתונים בזמן אמת במעבדי מיקרו מודרניים ובמכשירי מחשוב במהירות גבוהה.

חסרונות

עם זאת, תוספים מלאים מציגים גם חסרונות בולטים:

מורכבות בתכנון ויישום: תוספות מלאות כוללות שערי לוגיקה מרובים והתפשטות נשיאה רב-דרגית, מה שהופך את העיצוב שלהם למורכב.מורכבות זו לא רק מגדילה את עלויות הייצור אלא יכולה גם להשפיע על אמינות המעגלים.

בעיות עיכוב התפשטות: התפשטות נשיאה עשויה לעבור דרך מספר שערי לוגיקה, שכל אחד מהם להוסיף את העיכוב שלה.זה יכול להגביל את המהירות החישובית הכוללת במהלך פעולות בקנה מידה גדול, במיוחד במערכות מחשב נרחבות ובעיצוב של שילוב בקנה מידה גדול מאוד (VLSI) ומעבדים במהירות גבוהה.העיכוב יכול להפוך לצוואר בקבוק משמעותי בביצועים.

כדי להקל על סוגיות אלה, המהנדסים חוקרים ברציפות עיצובים יעילים יותר במעגלים.האסטרטגיות כוללות שימוש בטכנולוגיות מהירות של שער לוגיקה, מיטוב פריסות המעגלים כדי לקצר את אורכי הנתיב, ופיתוח טכנולוגיות מתקדמות כמו תוספי נשיאה כדי למזער את העיכובים בהתפשטות הנשיאה.

יישומים של תוספים מלאים בהיגיון דיגיטלי

תוספות מלאות משמשות בהרחבה בהיגיון דיגיטלי, המוערכים בגמישותם ויעילותם, מה שהופך אותם למרכזיים לשלל משימות מחשוב ועיבוד נתונים.היישום שלהם משתרע מפעולות חשבון בסיסיות ועד עיבוד אותות מורכבים ובקרת מערכת.להלן מבט מפורט על כמה תחומי מפתח בהם תוספים מלאים הם אינטגרליים.

מעגלים אריתמטיים

אחד השימושים הפשוטים ביותר בתוספות מלאות הוא במעגלים אריתמטיים שבהם הם מבצעים תוספת בינארית.חיוני במיוחד בתוספת מספר סיביות, תוספות מלאות מנהלות רצפים בינאריים ארוכים יותר באמצעות מדור.בסידור זה, כל ADDER מלא מטפל בתוספת למיקום הסיביות שלה והסחיבה מהסביבה התחתונה, ואז מעבירה את הנשיאה החדשה למדר המלא של הסיביות הגבוהה הבאה.מפל זה מאפשר תוספת רב-סיביות מקיפה בכל מגוון הספרות.

עיבוד נתונים

תוספים מלאים ממלאים גם תפקיד מרכזי במשימות עיבוד נתונים מתקדמות כמו עיבוד אותות דיגיטלי (DSP) לסינון ושינוי פורייה, שם יש צורך בפעולות חשבון מדויקות ומהירות.בנוסף, בתחום אבטחת המידע, כולל הצפנת נתונים ואלגוריתמים לגילוי שגיאות ותיקון כמו בדיקות זוגיות ושיטת קוד בינה מחזורית (CRC), תוספות מלאות הן מכריעות לביצוע פעולות סיביות חיוניות.

דלפקים

במונים דיגיטליים, תוספים מלאים חיוניים ליישום פונקציות תוספת וגם ירידה, במיוחד במונים מודולריים וסינכרוניים.הם מנהלים במדויק נושאות ומשאלות כדי להבטיח ספירה מדויקת.

מרבבים (MUX) ו- DemultIplexers (demux)

אצל מרבבים ומרכיבים דמולטפלקסרים, תוספים מלאים ממלאים תפקיד קריטי בבחירת הערוצים ובהפצת נתונים.הם משתתפים בהיגיון שקובע אילו ערוצים משמשים לקלט ופלט נתונים, וקבלת החלטות על בסיס אותות בקרת לוגיקה.

טכנולוגיית זיכרון

בכתובת זיכרון, תוספות מלאות עוזרות לייצר אותות כתובת לגישה דינאמית למיקומי זיכרון.זה חשוב במיוחד בזיכרון דינאמי של גישה אקראית (DRAM) ובמערכות אחסון אחרות, בהן תוספים מלאים תומכים בחישובי כתובת מורכבים כדי לשפר את היעילות של גישה לזיכרון.

יחידות לוגיקה אריתמטיות (ALU)

לבסוף, כרכיבים בסיסיים של יחידות לוגיקה אריתמטית במעבדי מיקרו -מעבדים ומעבדי אות דיגיטליים, מוסיפים מלאים הם מכריעים.ה- ALU מטפל בכל פעולות החשבון וההיגיון, כאשר תוספים מלאים מבטיחים שנתונים מעובדים במהירות ובמדויק.

דוגמאות ליישומי ADDER מלאים

ניתן לבנות תוספות מלאות באמצעות שערי לוגיקה ותצורות שונות.כאן אנו חוקרים ארבעה יישומים שונים, המדגישים את ההתקנה והניואנסים התפעוליים שלהם.

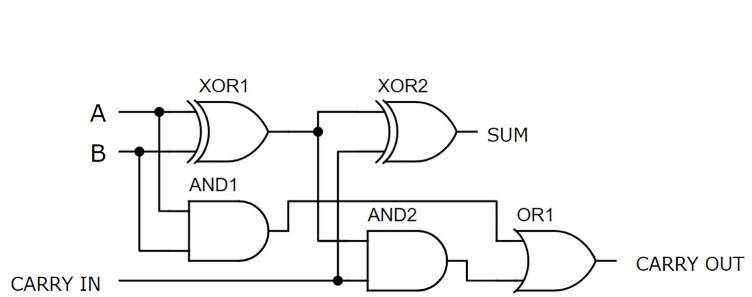
ADDER מלא שנבנה עם XOR, וגם או שערים

Full Adder Built with XOR, AND, and OR Logic Gates

איור 6: ADDER מלא בנוי עם XOR, ו או או בשערי לוגיקה

דוגמה זו מציגה אדר מלא שנבנה על קרש לחם באמצעות טרנזיסטורים נפרדים.התצורה כוללת חמישה שערי לוגיקה: שני שערי Xor, שניים ושערים, ושער אחד או שער, הדורשים סך הכל 21 טרנזיסטורים.הכניסות A ו- B מחוברות לשמאלית העליונה של הלחם, ומקבלות אספקת A +5V.כניסות אלה נשלטות על ידי שני מתגי מעבר.שתי נוריות LED בצד שמאל למעלה מצביעות על מצבי הכניסות A ו- B, ואילו שתי נוריות LED בצד ימין מציגות את היציאות.הנגדים המשמשים במעגל הם כולם 2.2K אוהם.כאשר תשומות A ו- B דולקות והעבירה כבויה, הפלט מראה ערך בינארי של 10, המייצג את הסכום 2 (1 + 1 + 0 = 10).שערי ה- Xor, שנבנו עם 12 הטרנזיסטורים הראשונים, מטפלים בסיכום הראשוני, ואילו המחצית התחתונה של לוח הלחם מכיל את השערים והשערים לפעולות נשיאה, חיווט מקודד צבע משפר את הבהירות ופתרון הבעיות.

ADDER מלא באמצעות NAND GATES

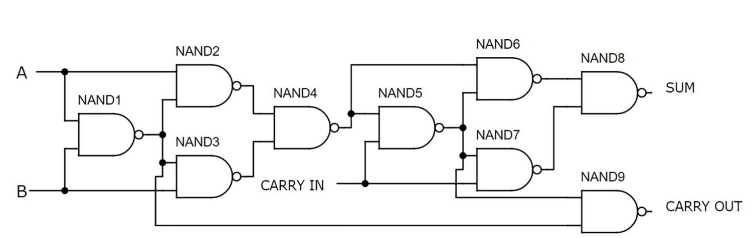
איור 7: ADDER מלא באמצעות NAND GATES

Adder מלא זה משתמש בתשעה שערי NAND, כאשר כל שער עשוי משני טרנזיסטורים, בסך הכל 18 טרנזיסטורים.שיטה זו היא בין הדרכים הפשוטות והיעילות ביותר לבניית ADDER מלא באמצעות רכיבים נפרדים.כל השערים מורכבים במחצית העליונה של לוח הלחם, ואילו מתגים תופסים את המחצית התחתונה.פונקציונליות המעגל מודגמת עם כניסות A ו- B והעברה, וכתוצאה מכך ערך בינארי פלט של 10, שווה ערך לעשרון 2.

Adder מלא עם NOR NOR

איור 8: ADDER מלא עם NOR NOR

מערך זה נבנה עם תשעה ולא שערים, וכל אחד מהם דורש שני טרנזיסטורים, משתמש גם ב -18 טרנזיסטורים בסך הכל.בניית ADDER מלא עם NOW Gates מציעה אלטרנטיבה טובה אך כרוכה בחיווט מורכב יותר בהשוואה לשערי NAND.כל טרנזיסטור בשערים NOR מבוסס, כאשר האספנים מחוברים על ידי חוטי מגשר כתומים כדי להבטיח חיווט מסודר ומאורגן.תצורה זו מוצגת עם כניסות A ו- B מופעלות וההפעלה מבוטלת, מה שמוביל ליציאות בהן הנשיאה פעילה והסכום כבוי.

סיכום

לאורך כל חיפוש זה של טכנולוגיית ADDER, החל מחצי תוספים בסיסיים ועד עיצובים מתוחכמים של ADDER, ניכר כי רכיבים אלה הם יסודיים לקידום האלקטרוניקה הדיגיטלית.המאפיינים התפעוליים ודוגמאות היישום סיפקו מדגישים את הרבגוניות והיעילות של תוספים במסגרות חישוביות שונות.על ידי בחינת המבנה ותפקודם של מוסיפים, במיוחד באמצעות טבלאות האמת והמשוואות האופייניות שלהם, אנו מקבלים תובנות חשובות לגבי יכולותיהם ואילוצי האילוצים שלהם.ידע זה מסייע לקידום תכנון של מערכות מחשוב יעילות ומהירות יותר.בסופו של דבר, תוספים לא רק מפשטים חישובים בינאריים מורכבים אלא גם מאפשרים להתפשטות הטכנולוגיה באזורים מגוונים כמו עיבוד נתונים, הקצאת זיכרון ועיבוד אותות דיגיטליים.עם התפתחות הטכנולוגיה הדיגיטלית, העידון והחדשנות המתמשכים בעיצוב Adder ימשיכו להיות אבן יסוד בפיתוח ארכיטקטורות חישוב מתקדמות יותר, מה שמבטיח כי רכיבים בסיסיים אלה יישארו בלב תכנון ויישום המערכת הדיגיטלית.

שאלות נפוצות [שאלות נפוצות]

1. מהו מעגל Adder מלא?

ADDER מלא הוא מעגל דיגיטלי שמוסיף שלושה ביטים בינאריים לייצור סכום ופלט נשיאה.הוא נועד לטפל בתוספת של שלוש תשומות: שני ביטים משמעותיים וקרוב אחד מתוספת קודמת.זה מאפשר להשתמש בו בשלבים רצופים כדי להוסיף מספרים בינאריים מרובי סיביות.

2. כמה, או, או, XOR במלאה מלא?

מוזר מלא טיפוסי מכיל:

שני שערי XOR לייצור הסכום.

שניים ושערים לתרום לחישוב הנשיאה.

אחד או שער כדי לסיים את תפוקת הנשיאה.

3. מהי קלט נשיאה במלוא המלא?

קלט הנשיאה (CIN) במדר מלא הוא סיבוב הנשיאה מתוספת הקטעים המשמעותיים הנמוכים הקודמים בתוספת בינארית רב-סיביות.זה מאפשר למלוא המלא לשקול נשיאה קודמת זו בעת חישוב הסכום הנוכחי ואת העבירה החדשה.

4. מדוע להשתמש במדר מלא במקום חצי מדר.

נעשה שימוש במלוא מלא במקום חצי מדרר מכיוון שהוא יכול להוסיף שלושה ביטים (כולל הנשיאה מתוספות קודמות), מה שהופך אותו למתאים לשרשור יחד כדי להוסיף מספרים מרובי סיביות.חצי סדר יכול להוסיף רק שני ביטים ואין לו הוראה להעברה, מה שמגביל את השימוש בו לצורות הפשוטות ביותר של תוספת בינארית ללא התפשטות נשיאה רציפה.

עלינו

ALLELCO LIMITED

Allelco הוא חד-פעמי מפורסם בינלאומי מפיץ שירותי רכש של רכיבים אלקטרוניים היברידיים, המחויב לספק שירותי רכש ושרשרת אספקה מקיפים לרכיבים לתעשיות הייצור וההפצה האלקטרוניות הגלובליות, כולל 500 מפעלי OEM העולמיים והמתווכים העצמאיים.
קרא עוד